© Sabine Kempken
Bogosort und fakultativer Wahnsinn
Stell dir vor, du willst ein gemischtes Kartenspiel sortieren (52 Karten), wie machst du das? Suchst du die kleinste Karte, dann die nächstkleinste und so weiter? Sortierst du erstmal in zwei Stapel mit eher hohen und eher tiefen Karten und teilst diese wiederum auf? Alles Schwachsinn! Der einzig wahre Sortieralgorithmus mischt die Karten einfach solange neu, bis sie zufällig in der richtigen Reihenfolge liegen! Dieser herrliche Algorithmus heißt Bogosort und braucht durchschnittlich 52! Mischversuche, um das Deck zu sortieren.
Warum 52!? Dafür kannst du hier ein bisschen Mathe ausklappen, du kannst aber auch direkt weiterlesen. :)
Es gibt 52! Reihenfolgen wie das Deck gemischt sein kann, denn für die erste Karte gibt es 52 Möglichkeiten, für die zweite 51, die dritte 50 und so weiter. Wir können es anhand eines kleineren Decks mit drei Karten (K1, K2 und K3) veranschaulichen.
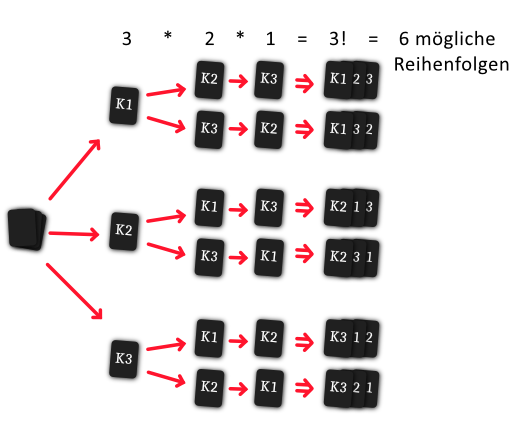Wir sehen 6 mögliche Reihenfolgen, also 3!. Immer, wenn eine Karte gezogen wurde, wird die Menge der übrigen Karten um eins reduziert. Wir starten also mit drei Möglichkeiten für die erste Karte, dann zweien für die zweite und nur noch einer Option für die dritte Karte.
Nur eine der Reihenfolgen ist die korrekte (K1,K2,K3), wir haben also bei jedem mal Mischen eine 1/6 Chance diese zufällig zu erhalten.
Die richtige Reihenfolge wird also im Durchschnitt mit Bogosort zufällig beim sechsten mal ziehen gefunden. Bei 52 Karten ist das Prinzip nicht anders, dieses Schaubild würde aber nicht ganz auf meine Website passen :).
Man muss also durchschnittlich 52! mal mischen, bis wir mit unserem befreundeten Einhorn zusammen Karten spielen können 🦄.
Der wahre Spaß beginnt jetzt, wenn wir uns überlegen, wie groß die Zahl 52! eigentlich ist. Stell dir vor, wir hätten einen Computer, der das Kartendeck einmal pro Sekunde mischt. Nimm dir kurz Zeit zu überlegen, wie lange er wohl durchschnittlich benötigt, bis uns das sortierte Deck in die Hand gedrückt wird? 🕑
Die Chance ist groß, dass deine Antwort etwas zu klein ist, ich nehme dich jetzt mit auf eine Reise.
Wir starten den Computer mit Bogosort und 52 unsortierten Karten und warten entspannte einhundert Jahre...
... der Computer rechnet noch. Wir gehen einen Meter und warten weitere einhundert Jahre...
... der Computer rechnet noch. Wir marschieren in einhundert-Jahre-Schritten um den gesamten Planeten...
... der Computer rechnet noch. Wir nehmen ein Löffelchen Salzwasser aus dem Atlantik und umrunden die Erde erneut...
... der Computer rechnet noch. Wir nehmen noch ein Löffelchen und laufen wieder um den Planeten...
... der Computer rechnet noch. Das machen wir weiter bis der Atlantik komplett leer ist...
... der Computer rechnet noch. Wir schaufeln ein Kilogramm Erde vom Mount Everest und füllen den Atlantik Löffel für Löffel wieder auf...
... der Computer rechnet noch. Wir schaufeln noch ein Kilogramm Erde vom Mount Everest und laufen so lange um den Planeten bis der Atlantik wieder leer ist...
... der Computer rechnet noch. So machen wir weiter bis der Mount Everest komplett weg ist...
... der Computer rechnet noch. Wir legen ein Blatt Papier auf den Boden und bauen den Mount Everest Kilogramm für Kilogramm vollständig wieder auf...
... der Computer rechnet noch. Wir bauen den Mount Everest wieder ab und legen ein weiteres Blatt auf das erste...
... der Computer rechnet noch. Wenn nach vielem weiteren Everest Auf- und wieder Abbauen und noch viel viel mehr Löffelchen Salzwasser und noch viel viel viel mehr gegangenen Schritten der Papierstapel so weit aufgefüllt wurde, dass er bis zur Sonne reicht...
... rappelt das Ding immer noch!
Du glaubst mir nicht? Das hier ist 52!:
80 658 175 170 943 878 571 660 636 856 403 766 975 289 505 440 883 277 824 000 000 000 000
So viele Sekunden benötigt der Computer durchschnittlich, um das Deck mit Bogosort zu sortieren. Wieviele Sekunden davon hat unser Papierstapel gebraucht? Wir rechnen...
60 * 60 * 24 * 365 * 100
= 315 360 000 Sekunden in einhundert Jahren.
* 40 075 017 = 126 380 573 611 200 000 Sekunden pro Weltumdrehung in 1-Meter-Schritten.
* 41 284 649 700 000 000 000 = 5 217 577 710 423 455 996 640 000 000 000 000 000 Sekunden bis der Atlantik ausgelöffelt ist.
* 458 347 045 333 000 = 2 391 461 327 367 910 132 318 484 775 681 120 000 000 000 000 000 000 Sekunden bis der Mount Everest weggeschaufelt wurde.
* 1 495 000 000 000 000 = 3 575 234 684 415 025 647 816 134 739 643 274 400 000 000 000 000 000 000 000 000 000 000 Sekunden bis der Papierstapel steht.
Das sind etwa 5% von 52!, wir können also noch circa 19 weitere Papierstapel bis zur Sonne neben den ersten stellen bis uns die Sekunden ausgehen ^^.
Du siehst, selbst wenn ein Computer erfunden würde, der doppelt-, dreifach- oder auch 1 000 000 000-fach schneller wäre als der derzeitige Standard, wäre das nichtmal ein Atom eines Tropfens auf dem heißen Stein bei einem Algorithmus, der fakultative Laufzeit benötigt. Darum ist es sehr wichtig, Algorithmen zu implementieren, die effizienter sind.
In diesem Beispiel ist das natürlich sehr überspitzt dargestellt. Niemand würde auf die Idee kommen, zum Sortieren einer Datenmenge Bogosort zu verwenden, dafür gibt es bessere Lösungen (zB. Bubblesort, Mergesort oder Quicksort). Es gibt aber Probleme in der Informatik, für die gibt es bis heute keine effizienten Lösungen (=> keine Algorithmen mit polynomieller Laufzeit). Das Bekannteste dieser Probleme ist wohl das
Traveling Salesman Problem/Problem des Handlungsreisenden, bei dem eine ideale Reiseroute zum Verteilen von Paketen bestimmt werden soll. Es gibt noch 20 weitere offene Probleme dieser Art, für deren Lösung man von heute auf morgen reich und berühmt würde.
Ein spannender Nebeneffekt dieser unglaublich großen Zahl ist, dass du, wenn du selbst ein Kartendeck gut durchmischst, garantiert eine Reihenfolge in der Hand hälst, die in der gesamten Menschheitsgeschichte noch nie jemand vor dir hatte. :)
